Introduzione al Teorema di Bayes: Bayesian
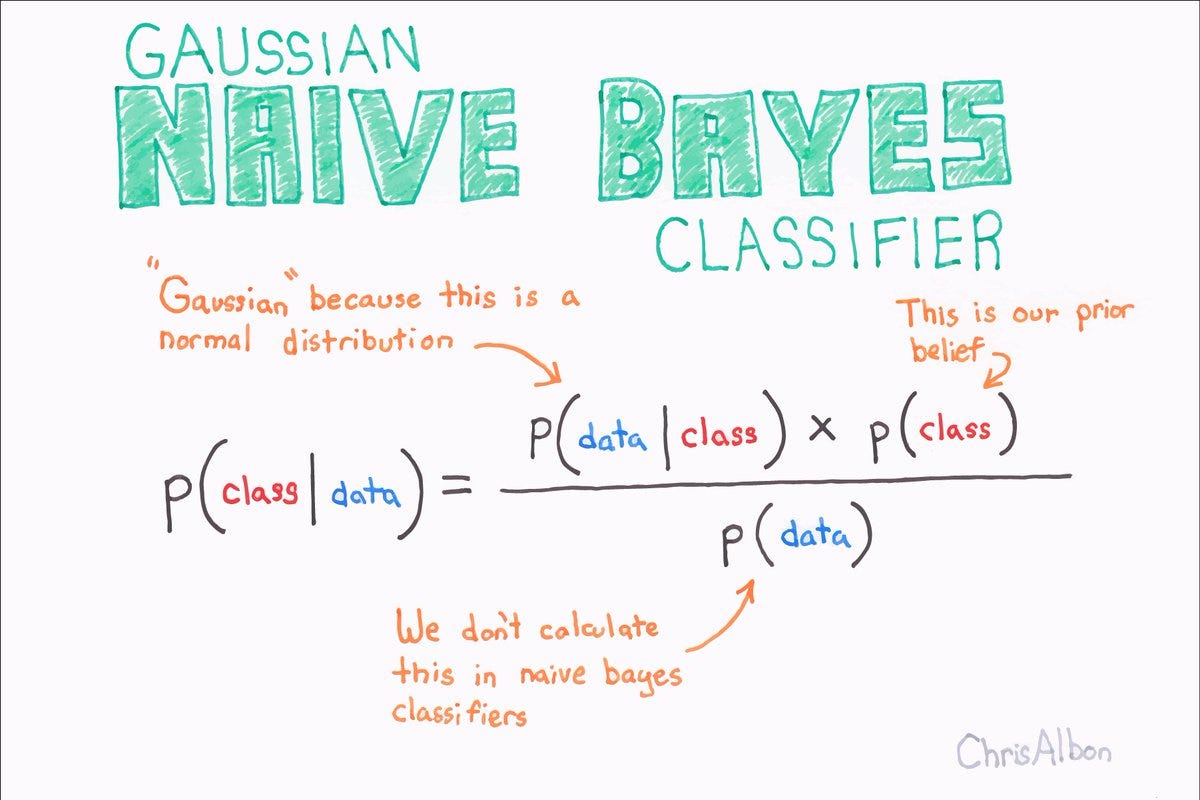
Immagina di dover valutare la probabilità di un evento, ma hai già a disposizione alcune informazioni aggiuntive. Il Teorema di Bayes ti fornisce uno strumento potente per aggiornare la tua comprensione di quell’evento alla luce di nuove evidenze. In sostanza, ti permette di calcolare la probabilità di un evento basandoti su ciò che già sai, e su nuove informazioni che potresti acquisire.
Il Teorema di Bayes è un’equazione che ci permette di calcolare la probabilità condizionata di un evento, ovvero la probabilità che l’evento si verifichi dato che un altro evento si è già verificato.
Applicazioni del Teorema di Bayes nella vita reale
Il Teorema di Bayes trova applicazione in diversi campi, tra cui:
- Medicina: Per esempio, in ambito medico, il Teorema di Bayes viene utilizzato per valutare la probabilità che un paziente abbia una determinata malattia, dato il risultato di un test diagnostico. Se il test è positivo, la probabilità di avere la malattia aumenta, ma la probabilità finale dipende anche dalla prevalenza della malattia nella popolazione.
- Finanza: Nel mondo finanziario, il Teorema di Bayes può essere applicato per analizzare i dati di mercato e prevedere l’andamento dei prezzi delle azioni. Ad esempio, un analista finanziario può utilizzare il Teorema di Bayes per aggiornare le proprie previsioni sui prezzi delle azioni, tenendo conto di nuove informazioni come i risultati finanziari di un’azienda.
- Intelligenza artificiale: Nel campo dell’intelligenza artificiale, il Teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i filtri antispam, i sistemi di riconoscimento facciale e i chatbot. Questi algoritmi utilizzano il Teorema di Bayes per aggiornare le proprie previsioni sulla base di nuove informazioni e migliorare le proprie prestazioni.
Importanza del Teorema di Bayes
Il Teorema di Bayes è uno strumento fondamentale nell’ambito della probabilità e dell’inferenza statistica, in quanto fornisce un metodo per aggiornare le nostre convinzioni sulla base di nuove evidenze. Ci permette di calcolare la probabilità di un evento in modo più preciso, tenendo conto di tutte le informazioni disponibili.
Il Teorema di Bayes è una formula che ci permette di calcolare la probabilità condizionata di un evento, ovvero la probabilità che l’evento si verifichi dato che un altro evento si è già verificato.
Applicazioni del Teorema di Bayes
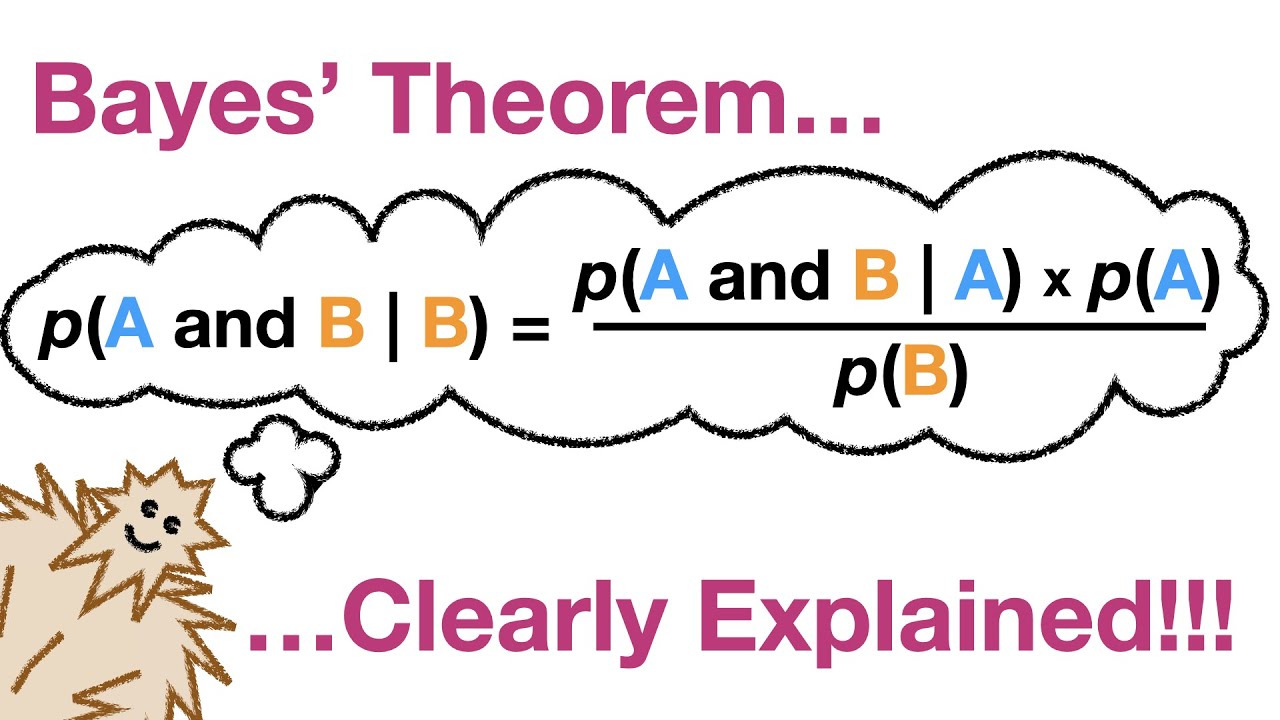
Il Teorema di Bayes, pur essendo un concetto matematico, trova un’ampia gamma di applicazioni in diverse discipline, dalla medicina alla finanza, dalla tecnologia alla scienza. Questo teorema, basato sulla probabilità condizionata, permette di aggiornare le nostre credenze sulla base di nuove informazioni, offrendo una potente chiave per comprendere e prevedere eventi futuri.
Applicazioni in ambito medico
Il Teorema di Bayes è uno strumento fondamentale nella diagnostica medica. Ad esempio, può essere utilizzato per calcolare la probabilità che un paziente abbia una specifica malattia, dato un risultato positivo a un test. Immaginate un test per il cancro al seno con un tasso di falsi positivi del 5%. Se una donna riceve un risultato positivo, il teorema di Bayes ci aiuta a capire quanto questo risultato sia realmente indicativo di un tumore, considerando la prevalenza del cancro al seno nella popolazione.
Applicazioni in ambito finanziario
Nel campo finanziario, il Teorema di Bayes viene utilizzato per analizzare il rischio e valutare le opportunità di investimento. Ad esempio, un fondo di investimento potrebbe utilizzare il teorema di Bayes per calcolare la probabilità di successo di un’azienda, considerando fattori come il suo bilancio, la sua posizione di mercato e le tendenze del settore. Questo permette di prendere decisioni di investimento più informate e di ridurre il rischio di perdite.
Applicazioni in ambito tecnologico
L’intelligenza artificiale e l’apprendimento automatico si basano ampiamente sul Teorema di Bayes. Ad esempio, i filtri antispam dei nostri sistemi di posta elettronica utilizzano questo teorema per identificare e bloccare le email indesiderate. I sistemi di riconoscimento vocale, come Siri o Alexa, utilizzano il teorema di Bayes per interpretare il linguaggio umano e rispondere in modo appropriato.
Applicazioni in ambito scientifico
Il Teorema di Bayes trova applicazioni in diverse aree della scienza, dalla fisica alla biologia. Ad esempio, in astronomia, può essere utilizzato per stimare la probabilità che un segnale radio provenga da una civiltà extraterrestre, considerando la probabilità di eventi naturali che potrebbero generare segnali simili.
Concetti chiave correlati

Il Teorema di Bayes si basa su concetti fondamentali di probabilità che sono essenziali per comprendere il suo funzionamento e le sue applicazioni. Questi concetti sono la probabilità a priori, la probabilità a posteriori e la probabilità condizionata.
Probabilità a priori, probabilità a posteriori e probabilità condizionata
Questi tre tipi di probabilità svolgono un ruolo cruciale nel contesto del Teorema di Bayes. La probabilità a priori rappresenta la nostra conoscenza iniziale di un evento prima di ricevere nuove informazioni. La probabilità a posteriori, invece, rappresenta la nostra conoscenza aggiornata di un evento dopo aver considerato nuove informazioni. La probabilità condizionata, infine, rappresenta la probabilità di un evento dato che un altro evento si è verificato.
La probabilità a priori è la probabilità di un evento prima che si verifichino nuove prove. La probabilità a posteriori è la probabilità di un evento dopo che si verificano nuove prove. La probabilità condizionata è la probabilità di un evento dato che un altro evento si è verificato.
Relazione tra i diversi tipi di probabilità
La probabilità a priori, la probabilità a posteriori e la probabilità condizionata sono strettamente correlate tra loro. La probabilità a posteriori viene calcolata utilizzando la probabilità a priori e la probabilità condizionata.
P(A|B) = [P(B|A) * P(A)] / P(B)
In questa formula, P(A|B) rappresenta la probabilità a posteriori di A dato B, P(B|A) rappresenta la probabilità condizionata di B dato A, P(A) rappresenta la probabilità a priori di A e P(B) rappresenta la probabilità di B.
Esempi, Bayesian
Consideriamo un esempio per illustrare la relazione tra questi concetti. Supponiamo di voler calcolare la probabilità che un paziente abbia il cancro al seno, dato che ha un risultato positivo a un test di screening. La probabilità a priori è la probabilità di avere il cancro al seno nella popolazione generale, mentre la probabilità condizionata è la probabilità di avere un risultato positivo al test di screening dato che si ha il cancro al seno. La probabilità a posteriori è la probabilità di avere il cancro al seno dato che si ha un risultato positivo al test di screening.
Utilizzando il Teorema di Bayes, possiamo calcolare la probabilità a posteriori tenendo conto della probabilità a priori e della probabilità condizionata. Questo ci permette di aggiornare la nostra conoscenza iniziale di un evento, tenendo conto di nuove informazioni.
Bayesian inference, with its focus on updating beliefs based on new evidence, has become a cornerstone of modern data analysis. This approach, with its roots in probability theory, has found its way into numerous fields, from medicine to finance, and even in the realm of technology.
Take, for example, the work of Mike Lynch, a British tech tycoon , whose company Autonomy pioneered innovative data management solutions. Lynch’s success highlights how Bayesian principles can be applied to build robust and adaptable systems, driving innovation in the ever-evolving world of technology.
Bayesian reasoning, with its focus on updating beliefs based on evidence, finds a compelling parallel in the story of Mike Lynch’s autonomy. His company’s success, like a Bayesian model, was built on constantly adapting to new information and market shifts, demonstrating the power of iterative learning and decision-making.
